Nesse post você vai encontrar 10 exercícios sobre funções e portas lógicas. Vários deles vão abordar assuntos como circuitos, portas E, OU, NOT e suas variações. Algumas respostas estão no fim desse post, não deixe de contribuir com a nossa comunidade 🙂
Considere as seguintes expressões:
A) S = (( A + B )’ + (C + D)’)’
B) S = ( A + B’ + C ) . ( A + B + C’ )’
C) S = ( A + B )’ . C . ( A + C ). B’
D) S = (( A + B )’ . C ) + (( B . C )’ . ( A’ + ( B . D ) ))
1) Desenhe o circuito correspondente as expressões
2) Construa a tabela da verdade para cada expressão
Considere a seguinte tabela da verdade:
|
A
|
B
|
C
|
S
|
|
0
|
0
|
0
|
0
|
|
0
|
0
|
1
|
0
|
|
0
|
1
|
0
|
0
|
|
0
|
1
|
1
|
1
|
|
1
|
0
|
0
|
0
|
|
1
|
0
|
1
|
1
|
|
1
|
1
|
0
|
1
|
|
1
|
1
|
1
|
1
|
3) Obtenha a equação booleana correspondente a tabela da verdade.
4) Determine as expressões das funções lógicas dos circuitos abaixo:
a) Circuito 1
b) Circuito 2
c) Circuito 3
5) Determine as expressões booleanas a partir das seguintes tabelas da verdade
a) Tabela 1
|
A
|
B
|
C
|
S
|
|
0
|
0
|
0
|
1
|
|
0
|
0
|
1
|
0
|
|
0
|
1
|
0
|
0
|
|
0
|
1
|
1
|
1
|
|
1
|
0
|
0
|
1
|
|
1
|
0
|
1
|
0
|
|
1
|
1
|
0
|
0
|
|
1
|
1
|
1
|
1
|
b) Tabela 2
|
A
|
B
|
C
|
D
|
S
|
|
0
|
0
|
0
|
0
|
0
|
|
0
|
0
|
0
|
1
|
1
|
|
0
|
0
|
1
|
0
|
1
|
|
0
|
0
|
1
|
1
|
0
|
|
0
|
1
|
0
|
0
|
0
|
|
0
|
1
|
0
|
1
|
0
|
|
0
|
1
|
1
|
0
|
0
|
|
0
|
1
|
1
|
1
|
1
|
|
1
|
0
|
0
|
0
|
0
|
|
1
|
0
|
0
|
1
|
1
|
|
1
|
0
|
1
|
0
|
0
|
|
1
|
0
|
1
|
1
|
0
|
|
1
|
1
|
0
|
0
|
1
|
|
1
|
1
|
0
|
1
|
0
|
|
1
|
1
|
1
|
0
|
0
|
|
1
|
1
|
1
|
1
|
1
|
6) Mostre que este circuito é um OU EXCLUSIVO
7) Mostre que o circuito é um circuito coincidência
8) Esquematize o circuito coincidência usando a porta NOU.
9) Esquematize o circuito OU EXCLUSIVO utilizando somente 4 portas NE.
10) Esquematize o circuito COINCIDENCIA, utilizando apenas 4 portas NOU.
Respostas
Exercício 1)
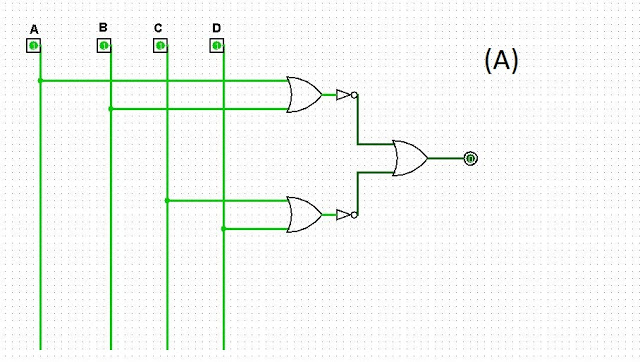
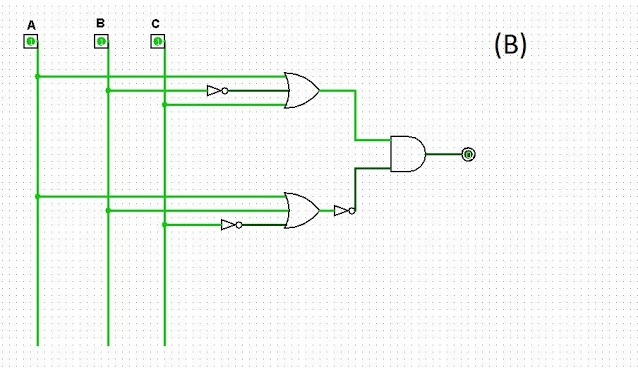
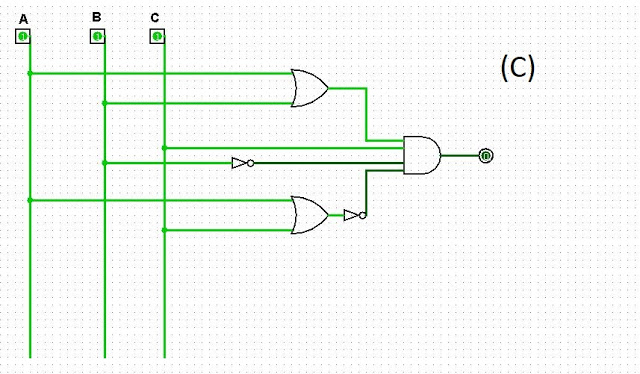
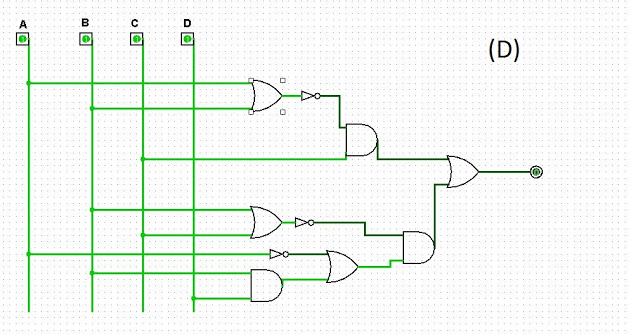
Exercício 2)
A) Primeiro Circuito
| A | B | C | D | (A + B) ‘ | (C + D)’ | S |
|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 1 | 1 | 1 |
| 0 | 0 | 0 | 1 | 1 | 0 | 1 |
| 0 | 0 | 1 | 0 | 1 | 0 | 1 |
| 0 | 0 | 1 | 1 | 1 | 0 | 1 |
| 0 | 1 | 0 | 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 1 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 0 | 1 | 1 |
| 1 | 0 | 0 | 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 | 0 | 0 | 0 |
| 1 | 1 | 1 | 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 | 0 | 0 | 0 |
B) Segundo Circuito
| A | B | C | (A+B’+C) | (A+B+C’)’ | S |
|---|---|---|---|---|---|
| 0 | 0 | 0 | 1 | 0 | 0 |
| 0 | 0 | 1 | 1 | 1 | 1 |
| 0 | 1 | 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 1 | 0 | 0 |
| 1 | 0 | 0 | 1 | 0 | 0 |
| 1 | 0 | 1 | 1 | 0 | 0 |
| 1 | 1 | 0 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 | 0 | 0 |
C) Terceiro Circuito
| A | B | C | (A + B)’ | (A + C) | S |
|---|---|---|---|---|---|
| 0 | 0 | 0 | 1 | 0 | 0 |
| 0 | 0 | 1 | 1 | 1 | 1 |
| 0 | 1 | 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 | 1 | 0 |
| 1 | 0 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 | 1 | 0 |
| 1 | 1 | 1 | 0 | 1 | 0 |
D) Quarto Circuito
| A | B | C | D | (A + B)’ | (B . C)’ | (B. D) | ( A + B )’ . C ) | ( B . C )’ . ( A’ + ( B . D )) | S |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 |
| 0 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 1 | 1 |
| 0 | 0 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 1 |
| 0 | 0 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 |
| 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 | 0 | 1 | 1 | 0 | 1 | 1 |
| 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 | 0 | 1 | 0 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| 1 | 1 | 0 | 1 | 0 | 1 | 1 | 0 | 1 | 1 |
| 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 0 |
- As respostas para os exercícios sobre funções e portas lógicas ainda estão em construção… se você resolveu algum desses exercícios e quer compartilhar com a comunidade entre em contato conosco.





Bom dia amigo
tem como me disponibilizar as respostas dos exercicios?
Boa tarde amigo, poderia disponibilizar as repostas para corrigir o mais rápido possível.
pois estou usando seu material como de estudo para uma prova
Boa noite… as respostas não estão disponibilizadas ainda?
poderia me mandar o gabarito
Olá, Vinicius!
Me chamo Pim e tenho 15 anos, e fiquei admirado em saber mais à fundo o mundo dos circuitos elétricos. Então devo dizer que seu conteúdo serviu de enorme ajuda pra mim, ficou super objetivo. Depois de estudar um pouco sobre o assunto, voltei pra realizar as atividades e logo após revisar as respostas. Felizmente me saí muito bem, mas percebi que há alguns errinhos que precisam ser corrigidos nas respostas aqui no site… se for possível, eu adoraria ajudar indicando onde está errado.
Olá Pim,
Fique a vontade para fazer contato comigo pelo e-mail: [email protected]
Você pode enviar as correções para mim que irei publicar por aqui!
eu adoraria compartilhar também sua contribuição
Olá, tudo bem? Estava fazendo esses exercícios para fixação e notei que no exercício 1, na letra D, não temos “B+C” e sim “B.C”, poderia me explicar, pf?!