As árvores no mundo da computação são estruturas de dados genéricas que ajudam a solucionar vários problemas. Árvore binária, Arvore B, Arvore AVL, Arvore rubro negra, são variações dessa estrutura. Outro assunto bastante recorrente na área são as operações de busca dentro dessas estruturas, essas operações envolvem algoritmos recursivos e costumam dar um nó na nossa cabeça.
Nesse post você vai encontrar vários exercícios sobre arvores e suas variações. Além disso, todos fizemos questão de exercícios resolvidos de arvore para apoiar seu aprendizado.
Atenção: todas as questões desse artigo foram aplicadas na POSCOMP e são de domínio público. Esse artigo tem a finalidade apoiar o ensino de computação e foram publicadas aqui com fim exclusivamente educativo.
Exercícios
1) [POSCOMP 2016 – FUNDATEC] Considere a árvore binária da figura a seguir:
Os resultados das consultas dos nós dessa árvore binária em pré-ordem e pós-ordem são, respectivamente:
- A) (2 4 6 8 12 16) e (2 6 8 4 16 12).
- B) (12 4 2 8 6 16) e (2 4 6 8 12 16).
- C) (2 6 8 4 16 12) e (12 4 2 8 6 16).
- D) (2 4 6 8 12 16) e (12 4 2 8 6 16).
- E) (12 4 2 8 6 16) e (2 6 8 4 16 12).
Resposta:
Em pré-ordem percorre-se primeiro visitando a raiz e depois a sub-árvore da esquerda depois da direita. Ou seja: 12, 4, 2, 8 ,6 16
Em pós-ordem a raiz é a ultima a ser visitada: Sendo assim: 2,6,8,4,16,12
Resposta correta (E)
2) [POSCOMP 2016 – FUNDATEC] A operação de destruição de uma árvore requer um tipo de percurso em que a liberação de um nó é realizada apenas após todos os seus descendentes terem sido também liberados. Segundo essa descrição, a operação de destruição de uma árvore deve ser implementada utilizando o percurso
- A) em ordem.
- B) pré-ordem.
- C) central.
- D) simétrico.
- E) pós-ordem.
Resposta:
Considerando que a raiz das árvores contém o ponteiro para os dois nós associados (sub-árvore da esquerda e sub-árvore da direita) então é necessário visitar todas subárvores e liberando os nós folha e posteriormente os nós raiz. Ou seja, esse percurso deve deixar a raiz por ultimo, caracterizando o percurso pós-ordem
Resposta correta (E)
3) [POSCOMP 2016 – FUNDATEC] Uma árvore balanceada T que armazena n chaves é uma árvore binária de pesquisa na qual
- A) A diferença entre as alturas de suas subárvores permanece constante em todo o caso, após inserções ou remoções de chaves.
- B) As operações de inserção e remoção de chaves em nodos internos v de T seguem um padrão linear de tempo de execução.
- C) A propriedade da altura/balanceamento é determinada pela extensão do caminho mais curto entre um nodo interno v até o nodo raiz de T.
- D) A variação da altura dos nodos filhos de cada nodo interno v de T é de, no máximo, uma unidade.
- E) o tempo de execução para todas as operações fundamentais sobre cada nodo interno v de T se mantém constante.
Resposta:
Existem diversos tipos de árvores balanceadas (técnicas para manter o balanceamento). Uma árvore é balanceada se a diferença de altura entre duas sub-árvores difere em apenas 1 unidade.
Resposta correta (D)
4) [POSCOMP 2015 – CENTRO DE SELEÇÃO – UFG] Considere T uma árvore binária cheia, em que n, ne, ni e h representam o número de nós, o número de nós externos, o número de nós internos e a altura de T, respectivamente. Portanto, a essa árvore T aplica-se a seguinte propriedade:
- (A) ni = ne + 1
- (B) h – 1 ≤ ne ≤ 2^h
- (C) h + 1 ≤ ni ≤ 2^h
- (D) log(n+1) ≤ h ≤ n – 1
- (E) 2h + 1 ≤ n ≤ 2^h+1 – 1
Resposta:
O número de nós de uma árvore cheia é dado por: 2^h+1 – 1.
2h + 1 representa 2 vezes a altura da arvore – 1, não existe possibilidade desse valor ser > que o número de nós.
Resposta correta (E)
5) [POSCOMP 2015 – COPS – UEL] Sobre árvores binárias, considere as afirmativas a seguir
.I. Qualquer nó de uma árvore binária é raiz de, no máximo, outras duas subárvores comumente denominadas subárvore direita e subárvore esquerda.
II. Uma dada árvore binária A armazena números inteiros e nela foram inseridos 936 valores não repetidos. Para determinar se um número x está entre os elementos dessa árvore, tal número será comparado, no máximo, com 10 números contidos na árvore A.
III. Uma dada árvore binária de busca A armazena números inteiros e nela foram inseridos 936 valores não repetidos. Para determinar se um número x está entre os elementos dessa árvore, serão feitas, no máximo, 10 comparações.
IV. Uma dada árvore binária de busca A armazena números inteiros e nela foram inseridos 936 valores não repetidos. Supondo que r seja o nó raiz da árvore A e que sua subárvore esquerda contenha 460 elementos e sua subárvore direita possua 475 elementos. Para determinar se um número x pertence a essa árvore, serão feitas, no máximo, 476 comparações.
Assinale a alternativa correta.
- a) Somente as afirmativas I e II são corretas.
- b) Somente as afirmativas I e IV são corretas.
- c) Somente as afirmativas III e IV são corretas.
- d) Somente as afirmativas I, II e III são corretas.
- e) Somente as afirmativas II, III e IV são corretas.
Resposta:
I. Qualquer nó de uma árvore binária é raiz de, no máximo, outras duas subárvores comumente denominadas subárvore direita e subárvore esquerda.
Correta – não é possível que uma árvore binária tenha mais de duas subárvores
II. Uma dada árvore binária A armazena números inteiros e nela foram inseridos 936 valores não repetidos. Para determinar se um número x está entre os elementos dessa árvore, tal número será comparado, no máximo, com 10 números contidos na árvore A.
Errada – isso só seria real se a arvore estivesse balanceada, onde o tempo de busca é log(n).
III. Uma dada árvore binária de busca A armazena números inteiros e nela foram inseridos 936 valores não repetidos. Para determinar se um número x está entre os elementos dessa árvore, serão feitas, no máximo, 10 comparações.
Errado – a arvore precisaria estar balanceada
IV. Uma dada árvore binária de busca A armazena números inteiros e nela foram inseridos 936 valores não repetidos. Supondo que r seja o nó raiz da árvore A e que sua subárvore esquerda contenha 460 elementos e sua subárvore direita possua 475 elementos. Para determinar se um número x pertence a essa árvore, serão feitas, no máximo, 476 comparações.
Correta – o ultimo número possível é o 475, sendo assim, não existe possibilidade de haver mais de 476 comparações.
Resposta correta (B)
6) [POSCOMP 2013 – COPS – UEL] Considere um grafo não dirigido G = (V,E), onde V é o conjunto de vértices e E o conjunto de arestas, no qual cada aresta possui um peso. G é uma instância para o Problema do Caixeiro Viajante (PCV), onde cada um de seus vértices são cidades e cada uma de suas arestas corresponde à ligação entre essas cidades. O peso de cada aresta corresponde à distância entre as duas extremidades. A árvore de busca, a seguir, corresponde à busca pela solução realizada por um algoritmo para o PCV. Sabendo-se que a busca pela solução ocorreu por profundidade, os nós da árvore de busca são analisados, explorando os “filhos” mais à esquerda primeiro (vértices com menor número).
Com base na estratégia de “poda” a ser utilizada para melhorar o desempenho e na análise das características da árvore de busca sobre a instância G, atribua V (verdadeiro) ou F (falso) às afirmativas a seguir.
( ) Ao encontrar o primeiro melhor caminho, deve-se registrá-lo, para não analisar caminhos que possuam mais vértices que este.
( ) Durante a abertura dos nós na árvore de busca, parar de seguir o caminho quando um ciclo é pior que o melhor encontrado até então.
( ) Manter o ciclo hamiltoniano de menor custo encontrado até então. Se, durante a busca, o caminho analisado ultrapassar este menor custo, parar tentativa por aquele caminho.
( ) Manter a distância atual do caminho percorrido e evitar abrir nós que a ultrapassem.
( ) Não realizar caminhos inversos aos que já foram analisados.Assinale a alternativa que contém, de cima para baixo, a sequência correta.
- a) V, V, F, V, F.
- b) V, F, V, F, V.
- c) F, V, F, V, F.
- d) F, V, F, F, V.
- e) F, F, V, F, V.
Resposta:
Resposta correta (E)
7) [POSCOMP 2013 – COPS – UEL] Observe a Árvore Binária de Busca (ABB) a seguir.
Assinale a alternativa que apresenta, corretamente, a sequência de inserção que gera essa ABB.
- a) 30, 15, 40, 10, 20, 60, 80
- b) 30, 15, 40, 10, 20, 80, 60
- c) 30, 15, 60, 10, 20, 40, 80
- d) 30, 60, 20, 80, 15, 10, 40
- e) 30, 60, 40, 10, 20, 15, 80
Resposta:
É preciso inserir os nós raiz primeiro, a seguir inserir as folhas.
Resposta correta (C)
8) [POSCOMP 2013 – COPS – UEL] Quanto à análise de algoritmos, considere as afirmativas a seguir.
I. A programação dinâmica pode levar a soluções eficientes para algoritmos recursivos com complexidade exponencial.
II. Os algoritmos tentativa e erro são impraticáveis com solução recursiva, pois são aplicados exaustivamente.
III. Um algoritmo recursivo tem tempo de execução inferior à codificação iterativa para a solução do mesmo problema.
IV. Uma árvore binária de pesquisa é adequada para a solução de problemas de natureza recursiva. Assinale a alternativa correta.
- a) Somente as afirmativas I e II são corretas.
- b) Somente as afirmativas I e IV são corretas.
- c) Somente as afirmativas III e IV são corretas.
- d) Somente as afirmativas I, II e III são corretas.
- e) Somente as afirmativas II, III e IV são corretas.
Resposta:
Os algoritmos de força bruta (tentativa e erro) são mesmo impraticáveis usando recursão. O tempo de execução de uma solução recursiva é maior do que a iterativa.
Resposta correta (B)
9) [POSCOMP 2012 – COPS – UEL] Um problema das árvores binárias de buscas convencionais é que a disposição dos elementos pode ficar semelhante à de uma estrutura linear, na qual as árvores criam uma profundidade maior que sua largura, como ocorre, por exemplo, em inserção de chaves em ordem crescente. Em árvores com essa característica, não há ganho substancial quanto ao tempo de busca de uma lista, por exemplo. As árvore AVL e SBBsão árvores projetadas para evitar esse problema e balancear o tempo de busca a seus elementos. Quanto às árvores AVL e SBB, assinale a alternativa que apresenta, corretamente, suas características.
- a) Árvores AVL utilizam altura das subárvores como critério de balanceamento, enquanto árvores SBB utilizam orientação vertical e horizontal dos “apontadores” dos nós.
- b) Árvores AVL utilizam quatro tipos diferentes de algoritmos de balanceamento, enquanto árvores SBB utilizam apenas dois tipos genéricos (direita e esquerda), levando em consideração a origem e a propagação de uma violação.
- c) Árvores SBB utilizam alturas das subárvores como critério de balanceamento, enquanto árvores AVL utilizam orientação vertical e horizontal dos “apontadores” dos nós.
- d) Árvores SBB utilizam quatro tipos diferentes de algoritmos de balanceamento, enquanto árvores AVL utilizam apenas dois tipos genéricos (direita e esquerda), levando em consideração a origem e a propagação de umaviolação.e) As árvores AVL e SBB possuem diferença quanto à estrutura dos nós e à composição das chaves e das funções de busca, de inserção e de remoção.
Resposta:
Resposta correta (A)
10) [POSCOMP 2010 – COPS – UEL] Assinale a alternativa em que todas as propriedades de uma árvore vermelho e preto são verdadeiras.
- a) Todo nó é vermelho ou preto. A raiz pode ser vermelha ou preta. Todas as folhas são vermelhas.
- b) A raiz é preta. Todas as folhas são vermelhas. Para cada nó, todos os caminhos, desde um nó até as folhasdescendentes, contêm um mesmo número de nós pretos.
- c) Toda folha é preta. Todo nó é vermelho ou preto. A raiz é preta.
- d) Se um nó é vermelho, ambos os filhos são vermelhos. A raiz pode ser vermelha ou preta. Todas as folhas são pretas.
- e) Todas as folhas são vermelhas. Todo nó é vermelho ou preto. A raiz pode ser vermelha ou preta.
Resposta:
Resposta correta (C)
11) [POSCOMP 2010 – COPS – UEL] Os algoritmos a seguir representam os três caminhamentos para árvores binárias.
caminhamento(binário)
se binário.esquerda 6= NULL então caminhamento(binário.esquerda)
escrever binário.valor
se binário.direita 6= NULL então caminhamento(binário.direita)
caminhamento(binário)
escrever binário.dado
se binário.esquerda 6= NULL então caminhamento(binário.esquerda)
se binário.direita 6= NULL então caminhamento(binário.direita)
caminhamento(binário)
se binário.esquerda 6= NULL então caminhamento(binário.esquerda)
se binário.direita 6= NULL então caminhamento(binário.direita)
escrever binário.valor- a) pré-ordem, pós-ordem, em-ordem
- b) pré-ordem, em-ordem, pós-ordem
- c) pós-ordem, pré-ordem, em-ordem
- d) em-ordem, pré-ordem, pós-ordem
- e) em-ordem, pós-ordem, pré-ordem
Resposta:
Resposta correta (D)
12) [POSCOMP 2010 – COPS – UEL] Em uma Árvore B de ordem, temos que:
(i) cada nó contém no mínimo m registros (em+1 descendentes) e no máximo 2m registros (e 2m+1 descendentes), exceto o nó raiz que pode conter entre 1 e 2m registros;
(ii) todas os nós folha aparecem no mesmo nível.
Sobre Árvores B, é correto afirmar:
- a) O particionamento de nós em uma Árvore B ocorre quando um registro precisa ser inserido em um nócom 2m registros.
- b) O particionamento de nós em uma Árvore B ocorre quando um registro precisa ser inserido em um nó commenos de 2m registros.
- c) O particionamento de nós em uma Árvore B ocorre quando a chave do registro a ser inserido contém um valor(conteúdo) intermediário entre os valores das chaves dos registros contidos no mesmo nó.
- d) O particionamento de nós ocorre quando é necessário diminuir a altura da árvore.
- e) Em uma Árvore B, aumenta em um nível sua altura, toda vez que ocorre o particionamento de um nó.
Resposta:
Resposta correta (A)
13) [POSCOMP 2009] Considere uma árvore binária de busca T com n nós e altura h. A altura de uma árvore é o número máximo de nós de um caminho entre a raiz e as folhas. Analise as afirmativas a seguir:
I. h < 1 + log2 n
II. Todo nó que pertence à subárvore esquerda de um nó x tem valor maior que o pai de x.
III. Uma busca em ordem simétrica (in-order) em T produz uma ordenação crescente dos elementos de T.
Assinale a alternativa CORRETA:
- A) Apenas a afirmativa I está correta;
- B) Apenas a afirmativa II está correta;
- C) Apenas a afirmativa III está correta;
- D) Apenas as afirmativas I e II estão corretas;
- E) Apenas as afirmativas I e III estão corretas.
Resposta:
Resposta correta (C)
14) [POSCOMP 2009] Percorrendo a árvore binária a seguir em pré-ordem, obtemos que seqüência decaracteres?
- A) A C G F B E D
- B) G C F A E B D
- C) A B C D E F G
- D) D B E A F C G
- E) A B D E C F G
Resposta:
Resposta correta (E)
15) [POSCOMP 2009] Dado um conjunto C contendo n inteiros distintos, qual das seguintes estruturas dedados em memória principal permite construir um algoritmo para encontrar o valormáximo de C em tempo constante?
- A) Um vetor não ordenado.
- B) Um vetor ordenado.
- C) Uma árvore binária de busca balanceada.
- D) Uma lista encadeada simples ordenada em ordem crescente.
- E) Uma árvore rubro-negra.
Resposta:
(A) É falsa. A busca pelo valor máximo seria feita em tempo O(n), pois você precisaria verificar todos os elementos do vetor.
(B) É verdadeira. O valor máximo estará no final do vetor, portanto basta retornar o valor da última posição, algo que pode ser realizado em tempo O(1), pois o acesso aos elementos de um vetor pode ser feito em tempo constante.
(C) É falsa. A complexidade seria O(log n), isto é, a complexidade é proporcional à altura da árvore.
(D) É falsa. O valor máximo estará no último nó da lista, portanto, o acesso será realizado em tempo O(n). É claro, estamos considerando uma lista simples (sem nó cauda).
(E) É falsa. A justificativa é a mesma de C.
Resposta correta (B)
16) [POSCOMP 2009] Quais das seguintes propriedades não se aplicam a árvores rubro-negras?
- A) Todo nó é vermelho ou preto.
- B) Todo nó folha é preto.
- C) Se um nó é preto, ambos seus filhos são vermelhos.
- D) Se um nó é vermelho, ambos seus filhos são negros.
- E) Todos os caminhos simples entre um nó e suas folhas descendentes contêm omesmo número de nós pretos.
Resposta:
Resposta correta (E)
17) [POSCOMP 2009] Considere a árvore minimax abaixo, representando um jogo onde queremosmaximizar o valor da função de avaliação estática:
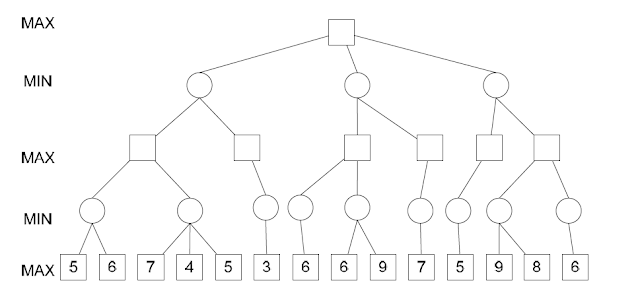
Assinale a alternativa que apresenta a quantidade de nós que não deverão servisitados em uma busca da melhor jogada se a estratégia de poda alfa-beta for utilizada.
- A) 5
- B) 8
- C) 9
- D) 10
- E) 11
Resposta:
Resposta correta (B)
18) [POSCOMP 2007] Seja T uma árvore AVL vazia. Supondo que os elementos 5, 10, 11, 7, 9, 3 e 6sejam inseridos nessa ordem em T, indique a sequência abaixo que corresponde a umpercurso de T em pós-ordem.
- (a) 3, 5, 6, 7, 9, 10 e 11.
- (b) 7, 5, 3, 6, 10, 9 e 11.
- (c) 9, 10, 7, 6, 11, 5 e 3.
- (d) 11, 10, 9, 7, 6, 5 e 3.
- (e) 3, 6, 5, 9, 11, 10 e 7.
Resposta:
Faça uma simulação de árvore AVL aqui
Resposta correta (E)
19) [POSCOMP 2007] Levando em conta as podas alfa-beta na árvore Mini-Max abaixo, assinale aalternativa que apresenta a quantidade de folhas que deverão ser visitadas
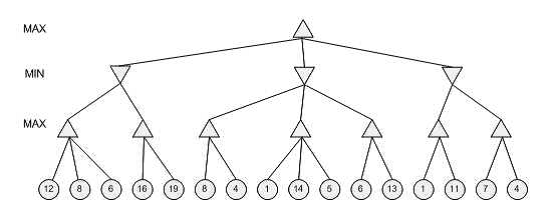
- (a) 7
- (b) 8
- (c) 10
- (d) 11
- (e) 13
Resposta:
Resposta correta (B)