George Kingsley Zipf (1902-1950), foi um americano linguista e filólogo que estudou estatísticas ocorrências em diferentes idiomas e deu nome ao que chamamos de “lei de zipf”. Esse pesquisador obteve seu bacharelado, mestrado e doutorado pela Universidade de Harvard, embora também tenha estudado na Universidade de Bonn e na Universidade de Berlim . Ele foi Presidente do Departamento Alemão e Professor Universitário (significando que ele poderia ensinar qualquer assunto que ele escolhesse) na Universidade de Harvard . Ele trabalhou com chineses e demográficos , e muito do seu esforço pode explicar propriedades da Internet , distribuição de renda dentro das nações e muitas outras coleções de dados.
Se você gosta desse tipo de conteúdo, não esqueça de acessar nossos artigos gratuitos sobre PLN.

As leis de Zipf
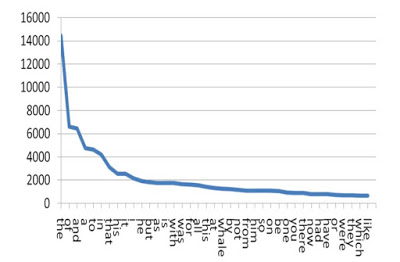
A primeira lei de Zipf segue a ideia de Estoup (2016) e diz que Contam-se quantas vezes cada palavra ocorre em um córpus grande, montando-se um ranque em função da frequência delas. Zipf afirma que há uma relação entre a frequência e a posição da palavra no ranque. Assim ele também infere a lei: Frequência x posição no ranque = constante k Em resumo, a observação de Zipf afirma que existem poucas palavras muito frequentes, um número significativo de palavras de frequência média e muitas palavras de frequência baixa. As palavras de alta frequência geralmente são as stopwords, já as palavras que tem baixa frequência são aquelas altamente específicas e erros de ortografia. Zipf também construiu uma visualização dessa sua teoria realizando a contagem de palavras no livro moby dick.
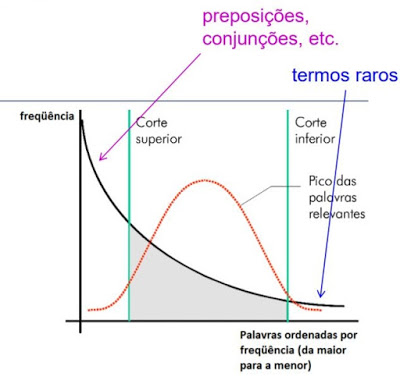
Os cortes de Luhn foram definidos por Luhn em 1958 e empiricamente definem cortes na curva onde são descartados os termos com alta frequência e os termos muito raros.
A grande questão é: onde realizar esses cortes?
Testando com LeroLero
Para colocar a prova a teoria de Zipf e Luhn, um experimento foi conduzido construindo um texto “dummy” gerado a partir do Gerador de LeroLero. Esse gerador monta sentenças aleatórias onde utilizaremos para construir nossa curva de Zipf e realizarmos os cortes.
Você pode acessar o arquivo completo do código-fonte aqui.
# Realiza a leitura do texto
arq = open('lerolero.txt', 'r',encoding='utf-8')
lerolero = arq.read()import nltk
# Separa as frases
sentLeroLero = nltk.sent_tokenize(lerolero)
# Separa cada palavra e conta sua frequência
word2count = {}
for data in sentLeroLero:
words = nltk.word_tokenize(data)
for word in words:
if word not in word2count.keys():
word2count[word] = 1
else:
word2count[word] += 1# realiza a ordenação do maior para o menor
sorted_words = sorted(word2count.items(), key=lambda kv: kv[1], reverse=True)import matplotlib
import matplotlib.pyplot as plt
# Dados para plotar
freq = frequency = [i[1] for i in sorted_words]
labels = list(range(0, len(sorted_words)))
fig, ax = plt.subplots()
ax.plot(freq, labels)
ax.set(xlabel='Words', ylabel='Frequency',
title='Zipf curve')
ax.grid()
plt.show()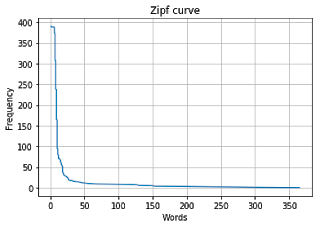
# Frequência x posição no ranque = constante k
zipfArray = []
for i in range(1,len(sorted_words)):
zipfArray.append(sorted_words[i][1] * i)
print(zipfArray)[299, 520, 600, 612, 750, 774, 896, 944, 603, 560, 561, 564, 572, 588, 540, 528, 561, 504, 513, 540, 567, 572, 598, 624, 625, 624, 648, 644, 609, 600, 620, 640, 660, 646, 665, 684, 703, 684, 702, 720, 738, 756, 774, 792, 810, 828, 846, 864, 882, 900, 918, 936, 901, 918, 935, 896, 912, 928, 944, 960, 976, 930, 945, 960, 975, 990, 1005, 952, 966, 980, 852, 864, 876, 888, 900, 912, 924, 936, 948, 880, 891, 902, 913, 924, 935, 946, 957, 968, 979, 990, 1001, 1012, 1023, 1034, 950, 960, 970, 980, 990, 1000, 1010, 1020, 1030, 1040, 1050, 1060, 1070, 1080, 1090, 1100, 1110, 1120, 1130, 1140, 1150, 1160, 1170, 1180, 1190, 1200, 1210, 1220, 1230, 1240, 1250, 1260, 1270, 1280, 1290, 1300, 1310, 1320, 1330, 1340, 1350, 1360, 1370, 1380, 1390, 1400, 1410, 1420, 1430, 1440, 1450, 1460, 1470, 1480, 1490, 1500, 1510, 1520, 1530, 1540, 1550, 1560, 1570, 1580, 1590, 1600, 1610, 1620, 1630, 1640, 1485, 1494, 1503, 1512, 1521, 1530, 1539, 1548, 1557, 1566, 1575, 1584, 1593, 1602, 1611, 1620, 1629, 1638, 1647, 1656, 1665, 1674, 1683, 1692, 1701, 1710, 1719, 1728, 1737, 1746, 1755, 1764, 1773, 1782, 1791, 1800, 1809, 1818, 1827, 1836, 1845, 1854, 1863, 1872, 1881, 1890, 1899, 1908, 1917, 1926, 1935, 1944, 1953, 1962, 1971, 1980, 1989, 1998, 2007, 2016, 2025, 2034, 2043, 2052, 2061, 2070, 2079, 2088, 2097, 2106, 2115, 2124, 2133, 1904, 1912, 1920, 1928, 1936, 1944, 1952, 1960, 1968, 1976, 1984, 1992, 2000, 2008, 2016, 2024, 2032, 2040, 2048, 2056, 2064, 2072, 2080, 2088, 2096, 2104, 2112, 2120, 2128, 2136, 2144, 2152, 2160, 2168, 2176, 2184, 2192, 2200, 2208, 2216, 2224, 2232, 2240, 2248, 2256, 2264, 2272, 2280, 2288, 2296, 2304, 2312, 2320, 2328, 2336, 2344, 2352, 2360, 2368, 2376, 2384, 2392, 2400, 2408, 2416, 2424, 2432, 2440, 2448, 2456, 2156, 2163, 2170, 2177, 2184, 2191, 2198, 2205, 2212, 2219, 2226, 2233, 2240, 2247, 2254, 2261, 2268, 2275, 2282, 2289, 2296, 2303, 2310, 2317, 2324, 2331, 2338, 2345, 2352, 2359, 2366, 2373, 2380, 2387, 2394, 2401, 2408, 2415, 2422, 2429, 2436, 2443, 2450, 2457, 2464, 2471, 2478, 2485, 2492, 2499, 2506, 2513, 2520, 2527, 2534, 2541, 2548, 2555, 2562, 2569, 2576, 2583, 2590, 2597, 2604, 2611, 2244, 2250, 2256, 2262, 2268, 2274, 2280, 2286, 2292, 2298, 2304, 2310, 2316, 2322, 2328, 389, 390]# Os cortes de luhn podem ser definidos empiricamente por tentativa e erro
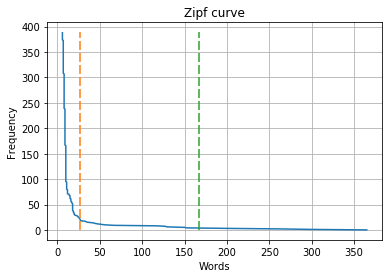
# Para esse texto os cortes foram definidos no indice 27 e 167
freq = frequency = [i[1] for i in sorted_words]
labels = list(range(0, len(sorted_words)))
corte_1x = [27] * 390
corte_1y = list(range(0,390))
corte_2x = [167] * 390
corte_2y = list(range(0,390))
fig, ax = plt.subplots()
ax.plot(freq, labels)
#cortes de luhn
ax.plot(corte_1x, corte_1y,dashes=[6, 2])
ax.plot(corte_2x, corte_2y,dashes=[6, 2])
ax.set(xlabel='Words', ylabel='Frequency',title='Zipf curve')
ax.grid()
plt.show()