Nesse post você encontra exercícios sobre algoritmo de ordenação para você praticar os conhecimentos adquiridos em sua universidade. Lembre-se que para resolve-los você precisará conhecer a teoria sobre os algoritmos e também compreender um pouco sobre complexidade de algoritmos.
Quer ver mais exercícios sobre estrutura de dados? Clique aqui.
Algumas respostas já estão presentes no fim do post, porém, esses exercícios estão ainda em construção. Sendo assim, se você conhece do assunto e quer compartilhar com a nossa comunidade seu conhecimento coloque nos comentários as resoluções. Posteriormente, irei atualizar o post com as melhores respostas.
1) [POSCOMP 2015 – CENTRO DE SELEÇÃO – UFG] Quais destes algoritmos de ordenação têm a classe de complexidade assintótica, no pior caso, em O(n.log n) ?
- (A) QuickSort, MergeSort, e HeapSort
- (B) QuickSort e SelectionSort
- (C) MergeSort e HeapSort
- (D) QuickSort e BubbleSort
- (E) QuickSort, MergeSort e SelectionSort
2) [POSCOMP 2015 – CENTRO DE SELEÇÃO – UFG] Analise o seguinte programa descrito na forma de pseudocódigo:
1. algoritmo
2. declare X[10], n, i, aux, flag numérico
3. para i ← 1 até 10 faça
4. leia X[i]
5. n ← 1
6. flag ← 1
7. enquanto (n ≤ 10 E flag = 1) faça
8. inicio
9. flag ← 0
10. para i ← 1 até 9 faça
11. inicio
12. se (X[i] < X[i+1]) então
13. inicio
14. flag ← 1
15. aux ← X[i]
16. X[i] ← X[i+1]
17. X[i+1] ← aux
18. fim_se
19. fim_para
20. n ← n + 1
21. fim_enquanto
22. para i ← 1 até 10 faça
23. escreva X[i]
24. fim_algoritmoO programa escrito acima realiza a ordenação decrescente de um vetor de números inteiros. O algoritmo implementado é de:
- (A) ordenação rápida.
- (B) ordenação por troca.
- (C) ordenação por seleção.
- (D) ordenação por inserção.
- (E) ordenação por intercalação
3) [POSCOMP 2013 – COPS – UEL] Sobre o comportamento assintótico do algoritmo de ordenação MergeSort (veja um exemplo de implementação abaixo), assinale a alternativa que apresenta, corretamente, sua complexidade.
MERGESORT(V, i, j)
Se (i<j) então
m = (i+j)/2;
MERGESORT(v, i, m);
MERGESORT(v, m+1, j);
MESCLAR(v, i, m, j);
Fim;- a) O(log n)
- b) O(n log n)
- c) O(n2)
- d) O(n3)
- e) O(2n)
4) [POSCOMP 2013 – COPS – UEL] Sobre a escolha adequada para um algoritmo de ordenação, considere as afirmativas a seguir.
I. Quando os cenários de pior caso for a preocupação, o algoritmo ideal é o Heap Sort.
II. Quando o vetor apresenta a maioria dos elementos ordenados, o algoritmo ideal é o Insertion Sort.
III. Quando o interesse for um bom resultado para o médio caso, o algoritmo ideal é o Quick Sort.
IV. Quando o interesse é o melhor caso e o pior caso de mesma complexidade, o algoritmo ideal é o Bubble Sort.
Assinale a alternativa correta:
- a) Somente as afirmativas I e II são corretas.
- b) Somente as afirmativas I e IV são corretas.
- c) Somente as afirmativas III e IV são corretas.
- d) Somente as afirmativas I, II e III são corretas.
- e) Somente as afirmativas II, III e IV são corretas.
5) [POSCOMP 2012 – COPS – UEL] Seja V um vetor de n inteiros não negativos, tal que o maior valor encontrado em V é m > 0. Com relação à ordenação de V , considere as afirmativas a seguir.
I. O tempo de execução dos algoritmos Quicksort e Mergesort para ordenar V é (n lg n) para qualquer valor de m.
II. Quando m = O(n), é possível ordenar V em tempo de execução O(n) no pior caso.
III. O tempo de execução de pior caso do Quicksort para ordenar V é O(n lg n) quando m = O(n).
IV. Para instâncias onde n = O(m), o algoritmo Countingsort é mais eficiente que o Mergesort, em função de n.
Assinale a alternativa correta.
- a) Somente as afirmativas I e II são corretas.
- b) Somente as afirmativas I e IV são corretas.
- c) Somente as afirmativas III e IV são corretas.
- d) Somente as afirmativas I, II e III são corretas.
- e) Somente as afirmativas II, III e IV são corretas.
Para responder às questões 6 e 7, considere a seguinte variante do algoritmo quicksort para ordenação de uma lista de inteiros x1, . . . , xn:
Algoritmo QS(x1,....xn)
Entrada: x1....xn inteiros
Saída: x1,....xn inteiros
Se n = 2 e x1 > x2, permutar x1 com x2.
Se n <= 2 retornar
i ← 2, j ← n,
Enquanto i < j,
Enquanto x1 >= xi e i < n + 1 incrementar i.
Enquanto x1 < xj, decrementar j.
Se i < j, permutar xi com xj.
Permutar x1 com xj.
QS(x1,....xj-1)
QS(xj+1, ... xn)6) [POSCOMP 2011 – COPS – UEL] Seja Φ(x1, …, xn) o número total de permutações de dois elementos durante a execução do algoritmo QS, inclusive durante as chamadas recursivas. Seja Φmax(n) o maior valor de Φ(x1, . . . , xn) para todas as listas possíveis de comprimento n. Sabendo que
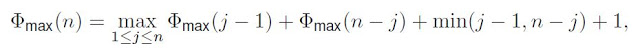
- a) Φmax(n) = n − 1.
- b) Φmax(n) está em o(n).
- c) Φmax(n) está em O(n log(n)), mas não em O(n).
- d) Φmax(n) está em O(n2), mas não em O(n log n).
- e) Φmax(n) > 2n.
7) [POSCOMP 2011 – COPS – UEL] Assinale a alternativa correta.
- a) O tempo de execução do algoritmo QS, no pior caso, para entradas de tamanho n, é de Φ(n log2(n)).
- b) O tempo de execução total do algoritmo para a entrada x1, . . . , xn é sempre de O(Φ(x1, . . . , xn)).
- c) O tempo de execução total do algoritmo QS para a entrada x1, . . . , xn não é proporcional à soma das vezes que cada uma das linhas foi executada.
- d) O tempo de execução do algoritmo QS, no pior caso, para entradas de tamanho n, é de Φ(n2).
- e) O número total de comparações do algoritmo QS, incluindo as chamadas recursivas, é de O(Φmax(n)) no pior caso.
8) [CS-UFG] Relacione as colunas:
Coluna 1
(I) Inserção
(II) Seleção
(III) QuickSort
(IV) ShellSort
(V) MergeSort (ou ordenação por fusão)
Coluna 2
(A) Encontra o menor elemento e o troca com a primeira posição, depois o segundo menor com a segunda posição e assim sucessivamente (n-1 vezes).
(B) As comparações e trocas são feitas baseadas em uma distância determinada (por exemplo: distância 4, onde o primeiro seria comparado com o quinto elemento, o segundo com o sexto, e assim sucessivamente), depois a distância é reduzida. Este processo se repete até que a distância seja 1 e as últimas comparações e trocas sejam efetuadas.
(C) A partir do segundo elemento, este deve ser colocado na sua posição correspondente (entre os elementos já analisados, como ao se organizarem as cartas de baralho na mão do jogador). Repete-se o procedimento até o último elemento.
(D) Escolhe-se um ponto de referência (pivô) e separam-se os elementos em 2 partes: à esquerda, ficam os elementos menores que o pivô, e à direita, os maiores. Repete-se este processo para os grupos de elementos formados (esquerda e direita) até que todos os elementos estejam ordenados.
(E) Divide-se o grupo de elementos ao meio, repete-se a divisão para cada um dos subgrupos, até que cada subgrupo tenha apenas 1 elemento. Nesse ponto, faz-se o reagrupamento dos subgrupos comparando os elementos e trocando, se necessário, para que eles fiquem ordenados. Repete-se este procedimento até restar um só grupo de elementos. Assinale a alternativa que contém a associação correta.
- a) I-A, II-D, III-B, IV-C, V-E.
- b) I-B, II-A, III-C, IV-E, V-D.
- c) I-B, II-A, III-E, IV-D, V-C.
- d) I-C, II-A, III-D, IV-B, V-E.
- e) I-D, II-E, III-B, IV-A, V-C.
9) [POSCOMP 2010 – COPS – UEL] Considere o problema de ordenação onde os vetores a serem ordenados, de tamanho n > 0, possuem [n/2] valores iguais a um número real x e [n=2] valores iguais a um outro número real y. Considere que os números reais x e y são conhecidos e fixos, porém estão distribuídos aleatoriamente no vetor a ser ordenado. Neste caso, é correto afirmar:
- a) Podemos ordenar estes vetores a um custo O(n).
- b) No caso médio, o Quicksort será o algoritmo mais eficiente para este problema, com um custo O(n log n).
- c) O algoritmo de ordenação por inserção sempre opera no melhor caso com um custo O(n).
- d) O limite inferior para esta classe de problema é Ω(n²) .
- e) O limite inferior para esta classe de problema é Ω(n logn).
10) [POSCOMP 2008] Os fragmentos de programas abaixo, enumerados 1, 2 e 3, são implementações para o problema de ordenação usando o algoritmo quicksort.
Programa 1
quicksort([],[]).
quicksort([Head|Tail],Sorted) :-
partition(Head, Tail, Left, Right), quicksort(Left,SortedL),
quicksort(Right,SortedR),
append(SortedL), [Head|Tail], [Head|Left], Right) :-
partition (Pivot, [], [] ,[]).
partition (Pivot, [Head|Tail],[Head|Left],Right) :-
Head <= Pivot, partition(Pivot,Tail,Left,Right).
Partition (Pivot, [Head|Tail],Left,Right).
Head > Pivot, partition(Pivot, Tail, Left, Right).
append([], List, List).
append ([Head|List1],List2,[Head|List3]) :-
append(List1,List2,List3).Programa 2
quicksort [] = []
quicksort (head:tail) = let pivot = head
left = [x|x <- tail,x < pivot]
right = [x|x <- tail, x >= pivot]
in quicksort left ++ [pivot] ++ quicksort rightPrograma 3
void quickSort( int a[], int l, int r){
int j;
if (l < r){
j = partition (a, l, r);
quickSort (a, l, j-1);
quickSort( a, j+1, r);
}
}
int partition( int a[], int l, int r){
int pivot, i, j, t;
pivot = a[l], i= l; j = r+1;
while(i < j) {
do ++i; while(a[i] <= pivot && i <= r);
do --j; while (a[j] < pivot);
if( i < j ) {
t = a[i]; a[i] = a[j]; a[j] = t;
}
}
t = a[l]; a[l] = a[j]; a[j] = t;
return j;
}Assinale a alternativa que enumera os paradigmas das linguagens com as quais os programas 1, 2 e 3 foram respectivamente implementados.
- A) Lógico, imperativo e funcional
- B) Imperativo, funcional e lógico
- C) Funcional, lógico e imperativo
- D) Lógico, funcional e imperativo
- E) Funcional, funcional e imperativo
Respostas
1) Resposta correta (C)
Nesse exercício você precisa lembrar qual é complexidade dos algoritmos de ordenação no pior caso. A wikipedia pode te ajudar Facilitando a sua consulta. Veja artigos completos sobre o quicksort, mergesort e heapsort. Observando que o quicksort no seu pior caso tem complexidade O(n²), podemos descartar todas as alternativas exceto a letra (C).
2) Nesse exercício você precisa compreender como funciona o algoritmo de troca (bubble sort). Nas linhas 12 até 17, percebemos que existe uma operação de troca dos números e ela se repete até o fim do vetor. Saiba mais clicando aqui. Veja a seguir um exemplo visual desse algoritmo:
3) Resposta correta:
Alternativa (B)
O merge sort, ou ordenação por mistura, é um exemplo de algoritmo de ordenação por comparação do tipo dividir-para-conquistar. Sua ideia básica consiste em Dividir (o problema em vários subproblemas e resolver esses subproblemas através da recursividade) e Conquistar (após todos os subproblemas terem sido resolvidos ocorre a conquista que é a união das resoluções dos subproblemas).
Como o algoritmo MergeSort usa a recursividade, há um alto consumo de memória e tempo de execução, tornando esta técnica não muito eficiente em alguns casos. Sua complexidade assintótica é O(n log n). Veja um exemplo visual do funcionamento desse método:
Veja uma explicação mais detalhada sobre a complexidade desse método clicando aqui.
4) Resposta correta:
Alternativa (D) I)
Para compreender sobre a complexidade dos algoritmos é preciso analisar sobre diversos aspectos, incluindo se os elementos estão ordenados. Veja uma tabela comparativa da complexidade de alguns algoritmos de ordenação:
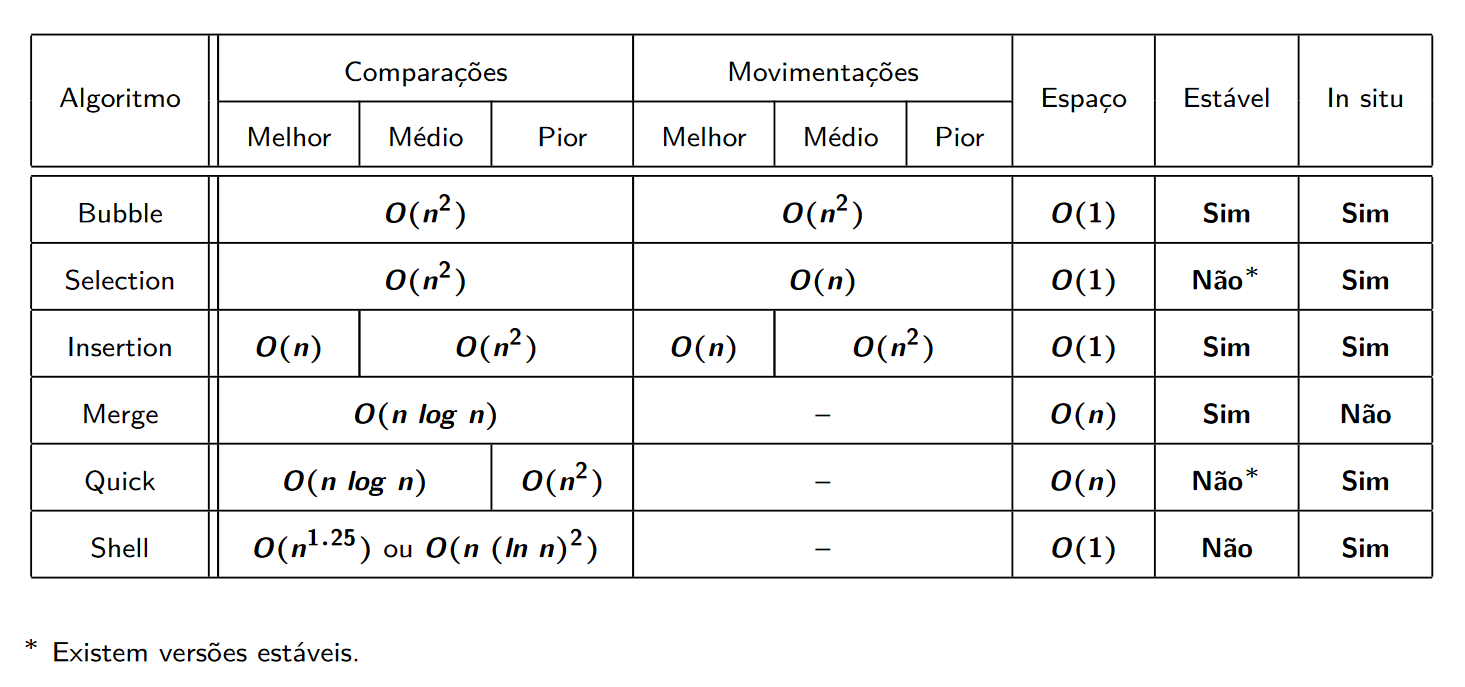
O heapsort mencionado na opção I possui complexidade O log (n) em todas as situações (melhor, medio, pior caso) O insertion sort possui seu melhor caso quando o array está ordenado. Veja uma referência aqui. O quicksort possui em caso médio e pior caso a complexidade O log (n). Veja uma referência aqui. Um tutorial muito legal você pode acessar aqui.
5) A
6) C
7) D
8) D
9) A
10) D
Obs: As respostas estão em desenvolvimento ainda, sendo assim, se você resolveu algum exercício ou sabe explicar uma resposta com mais detalhes coloque nos comentários que iremos atualizar o post 🙂






