Nessa aula iremos mostrar o que é e como funciona o k-means. implementar um exemplo simples utilizando o scikit-learn. Em mineração de dados, agrupamento k-means é um método de Clustering (agrupamento) que objetiva particionar n observações dentre k grupos onde cada observação pertence ao grupo mais próximo da média. Isso resulta em uma divisão do espaço de dados em um Diagrama.
O problema é computacionalmente difícil, no entanto, existem algoritmos heurísticos eficientes que são comumente empregados e convergem rapidamente para um local ótimo. Estes são geralmente semelhantes ao algoritmo de maximização da expectativa para misturas de distribuições gaussianas através de uma abordagem de refinamento iterativo utilizado por ambos os algoritmos. Além disso, ambos usam os centros de clusters para modelar dados, no entanto, a clusterização k-means tende a encontrar clusters de extensão espacial comparáveis enquanto o mecanismo de maximização da expectativa permite ter diferentes formas.
Breve história do algorítmo
O termo “k-means” foi empregado primeiramente por James MacQueen em 1967, embora a ideia remonta a Hugo Steinhaus em 1957. O “Standard algorithm” foi proposto primeiramente por Stuart Lloyd em 1957 como uma técnica para modulação por código de pulso, embora não tenha sido publicada fora dos laboratórios Bell até 1982. Em 1965, E.W.Forgy publicou essencialmente o mesmo método, é por isso que é por vezes referido também como Lloyd-Forgy. Uma versão mais eficiente foi proposta e publicada em Fortran por Hartigan e Wong, no período entre 1975 e 1979.
Ideia geral do algoritmo
Para entender o funcionamento desse algoritmo imagine que precisamos vamos separar um conjunto de pontos em um gráfico em 2 clusters (conjuntos). Considerando o algoritmo k-means, o K nesse caso será igual a quantidade de conjuntos que queremos dividir. O centróides é o ponto ponto mais central dos grupos que serão criados e ajudará a encontrará a similaridade dos dados.
Uma das formas de começar o algoritmo é iniciar processo é inserir o K pontos (centróides) aleatórios iniciais. Isso pode acontecer em qualquer lugar do plano, para que em seguida o algoritmo comece as iterações e encontre os resultados.
Em determinada iteração existe um ponto de equilíbrio onde existe mais mudança de pontos entre o gráfico e o centróide, fazendo com que o algoritmo pare a execução e chegue resultado esperado criando dois grupos. Quando um novo é incluído no gráfico, esse ponto já terá um grupo que atende aquela área e o algoritmo já saberá como tratar o dado novo.
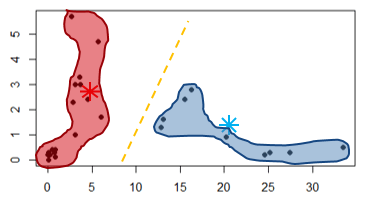
Veja o exemplo da figura acima, dois clusters (vermelho e azul) são criados que incluem vários pontos. Se um novo ponto for inserido do lado direito, provavelmente será incluído pelo cluster azul.
Implementando um exemplo de k-means em Python
A implementação mais básica do k-means que contém um vetor [X] que contém os pontos amostrados. O objetivo é classificar os pontos amostrados em clusters indicados pela variável K.
from sklearn.cluster import KMeans import numpy as np
X = np.array([[1, 2], [1, 4], [1, 0],[4, 2], [4, 4], [4, 0]]) kmeans = KMeans(n_clusters=2, random_state=0).fit(X) kmeans.labels_
array([0, 0, 0, 1, 1, 1])
kmeans.predict([[0, 0], [4, 4]])
array([0, 1])
kmeans.cluster_centers_
array([[1., 2.],
[4., 2.]])
Diferença entre KNN e K-means
O KNN faz parte do tipo de aprendizado denominado “supervisionado”, esse aprendizado precisa de exemplos previamente classificados para prever qual será a classificação de uma nova amostra. O K-means busca dividir em grupos amostras de acordo com um número de clusters pré-determinado, sendo assim, não precisa de exemplos pré-classificados.





